Monday, November 6, 2017
By: Matthew Doucette
A "sequel" to Random Pi, I thought why not try the same idea -- of estimating Pi with random numbers landing in and out of the unit-sphere -- with uniformly distributed numbers.
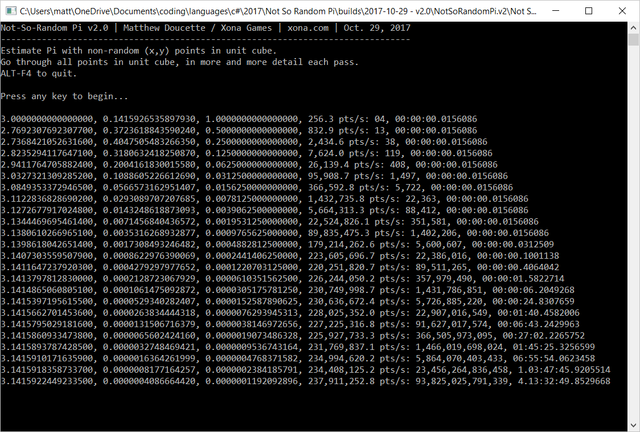
Not-So-Random Pi running up to 93,000,000,000,000 iterations.
Algorithm:
Similar but not the same as Random Pi, the idea is to chose evenly distributed numbers within the unit square (-1.0..1.0,-1.0..1.0) and measure the percentage of points lying inside the unit sphere. Using the area of a circule formula -- area = pi * radius^2 -- you can deduce the inside:total ratio multiplied by 4 is Pi.
This is known as the Monte Carlo method, although that method is usually choosing random numbers, not evenly distributed numbers.
From the output above you can see at first, only 4 numbers are chosen, at the edges of the unit square (-1.0..1.0,-1.0..1.0):
. .
. .
Then, the step is divided by two, breaking down the unit square into smaller pieces, so 9 numbers are chosen (total = 13 = 4+ 9):
. . .
. . .
. . .
Then, the step is divided by two again, so 25 numbers are chosen (total = 38 = 4 + 9 + 25):
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
And so on...
Algorithm Flaw:
The algorithm repeats the same points each phase. What I could have done is coded it to to be offsetted so that each phase it is sampling just as many points -- perhaps with one row and one column less -- without repeats.
Results:
After 4 days, 13 hours, 32 minutes, and 49.9 seconds, 93,825,025,791,339 samples were taken, which estimate pi to be 3.1415922449233500 which is off by 0.000000408666442, accurate to 99.9999591334%.
Calculation Time:
Each estimate takes approximately 4 times longer than the previous one, so the calculation times grows exponentially for each successive step. Based on the last two estimates, it is 3.94110053 times longer:
Assuming this value, we can estimate future values:
- <1s
- <1s
- <1s
- <1s
- <1s
- <1s
- <1s
- <1s
- <1s
- <1s
- <1s
- <1s
- <1s
- <1s
- 1.58 seconds
- 6.20 seconds
- 24.8 seconds
- 100.5 seconds
- 6.72 minutes
- 27 minutes
- 1.75 hours
- 6.93 hours
- 1.16 days
- 4.6 days
- 18.0 days (estimated)
- 70.9 days (estimated)
- 279.4 days (estimated)
- 3.0 years (estimated)
- 11.9 years (estimated)
- 46.8 years (estimated)
- 184.6 years (estimated)
- 727.4 years (estimated)
- 2,900 years (estimated)
- 11,300 years (estimated)
- 45,000 years (estimated)
- 175,000 years (estimated)
If I left it running, I would not likely be alive to see the 6th extra result. And it was about 100,000..200,000 years ago that we evolved into humans, so by the 12th extra result, a lot could happen to us on evolutionary time frames.
Unit Square:
P.S. The unit square is actually from (0.0..1.0,0.0..1.0) not (-1.0..1.0,-1.0..1.0).
Check out our other prototype work if you wish.
That is all.
About the Author: I am Matthew Doucette of Xona Games, an award-winning indie game studio that I founded with my twin brother. We make intensified arcade-style retro games. Our business, our games, our technology, and we as competitive gamers have won prestigious awards and received worldwide press. Our business has won $190,000 in contests. Our games have ranked from #1 in Canada to #1 in Japan, have become #1 best sellers in multiple countries, have won game contests, and have held 3 of the top 5 rated spots in Japan of all Xbox LIVE indie games. Our game engines have been awarded for technical excellence. And we, the developers, have placed #1 in competitive gaming competitions -- relating to the games we make. Read about our story, our awards, our games, and view our blog.
